在平面中描述立体——透视详解(上)

导言：
有些朋友喜欢用ps 做一些立体物件，或者画一些3维场景，却苦于形体不准确或者没有强烈的视觉冲击。这与没有良好的立体感有一定关系，尤其是透视的基础，对于我们这些不用3ds  max软件的 photoshop 爱好者来说学学透视满重要的。

记得大学学工程制图的时候学了一点~ 虽然忘了很多，但对现在的设计应用还是蛮有帮助的。
下次再画透视很强的东西，就可以先用画笔打个稿子了~ 这样就不会太走形。

一、透视图的意义
设计需要用图来表达构思。在广告艺术、建筑学、室内设计、雕塑设计、装饰设计和工业设计以及其他相关领域里，都是通过表现画将设计者的构思传达给使用者的，也就是通过图画来进行交流的。

对任何一位从事表现艺术设计的人来说，透视图都是最重要的。无论是从事美术、建筑、室内设计，都必须掌握如何绘制透视图，因为它是一切作图的基础。透视有助于形成真实的想象。而且它是建立在完美的制图基础之上的。

透视画，是把建筑物的平面、立面或室内的展开图，根据设计图资料，画成一幅尚未成实体的画面。将三度空间的形体转换成具有立体感的二度空间画面的绘图技法，并能真实地再现设计师的预想。

透视画，不但要注意材质感，对于画面的色面构成、构图等问题，透视画技法在绘图技法上负有很大的责任，因为优秀的透视画超越表面的建筑物说明图，具有另一方面的优异绘画性格。
在建筑、室内设计的表现画中，所表现的空间必须确切，因为对空间表现的失真会给设计者和用户造成错觉，并使各相关部位出现不协调感。

常画透视画的人们，不一定完全忠实于透视画法的作图过程，大都用简便方法的为多。这种方法不但省时，并能提高视觉效果，但这需要经过绘画和透视技法的训练后，才能如愿。它需要对立体造型的建筑物、室内空间有深度的理解和把握。

透视画和绘画、雕刻不同，不能用纯粹形态单独完成，不能视透视画为专门技术，而只学其技巧就自认为大功告成了，必须和原设计方案密切配合，掌握设计意图，这样才能充分表现设计者的思想构思。

 二、透视图
透视图即透视投影，在物体与观者之位置间，假想有一透明平面，观者对物体各点射出视线，与此平面相交之点相连接，所形成的图形，称为透视图。视线集中于一点即视点。

透视图是在人眼可视的范围内。在透视图上，因投影线不是互相平行集中于视点，所以显示物体的大小，并非真实的大小，有近大远小的特点。形状上，由于角度因素，长方形或正方形常绘成不规则四边形，直角绘成锐角或钝角，四边不相等。圆的形状常显示为椭圆（图01、02）。

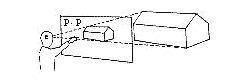
图01

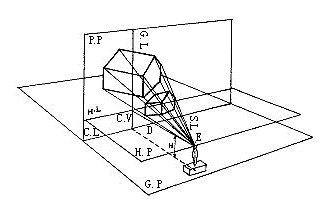
图02

透视术语：
P．P．画面 假设为一透明平面；
G．P．地面 建筑物所在的地平面为水平面；
G．L．地平线 地面和画面的交线；
E．视点 人眼所在的点；
H．P．视平面 人眼高度所在的水平面；
H．L．视平线 视平面和画面的交线；
H．视高 视点到地面的距离；
D．视距 视点到画面的垂直距离；
C．V．视中心点 过视点作画面的垂线，该垂线和视平线的交点；
S．L．视线 视点和物体上各点的连线；
C．L．中心线 在画面上过视心所作视平线的垂线。

#p#e#

三、透视的种类
1．一点透视：
物体的两组线，一组平行于画面，另一组水平线垂直于画面，聚集于一个消失点，也称平行透视。一点透视表现范围广，纵深感强，适合表现庄重、严肃的室内空间。缺点是比较呆板，与真实效果有一定距离（图03）。

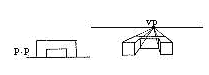
图03

2．二点透视：
物体有一组垂直线与画面平行，其他两组线均与画面成一角度，而每组有一个消失点，共有两个消失点，也称成角透视。二点透视图面效果比较自由、活泼，能比较真实地反映空间。缺点是，角度选择不好易产生变形（图04）。

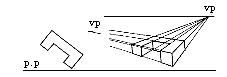
图04

3．三点透视：
物体的三组线均与画面成一角度，三组线消失于三个消失点，也称斜角透视。三点透视多用于高层建筑透视（图05）。

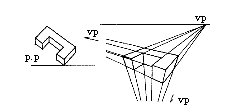
图05

四、透视的基本规律
1．凡是和画面平行的直线，透视亦和原直线平行。凡和画面平行、等距的等长直线，透视也等长。如图：AA’‖aa’，BB’‖bb’；AA’=BB’，aa’=bb’（图06）。

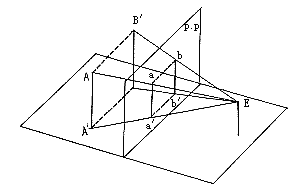
图06

2．凡在画面上的直线的透视长度等于实长。当画面在直线和视点之间时，等长相互平行直线的透视长度距画面远的低于距画面近的，即近高远低现象。当画面在直线和视点之间时，在同一平面上，等距，相互平行的直线透视间距，距画面近的宽于距画面远的，即近宽远窄。

如图：AA’的透视等于实长；cc’＜bb’＜AA’；cc’和 bb’的间距小于 bb’和AA’的间距（图07）。

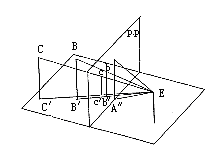
图07

3．和画面不平行的直线透视延长后消失于一点。这一点是从视点作与该直线平行的视线和画面的交点——消失点。和画面不平行的相互平行直线透视消失到同一点。

如图：AB和A’B’延长后夹角θ3＜θ2＜θ1，两直线透视消失于V点，AB‖A’B’（图08）。

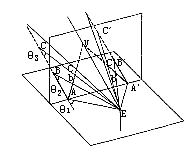
图08

#p#e#

五、透视的角度
人类的眼睛并非以一个消失点或二个消失点看东西，有时没有消失点，有时借用很多消失点看东西。这和照相机的光镜一样，由焦点调整法有时会使前面东西模糊不清，应该看到的东西却变成盲点。绘画和电影则是进行调整，把视觉上的特征有效地表现出来。透视画也应如此作适当的调整，否则就会出现失真现象。

如图：用两个消失点V1、V2的距离作为直径画圆形。越近于圆中心的，越看得自然，越远的越不自然，离开圆形，位于外侧的，使人看不出它是正方形和正六面体。平行透视法尽量限定对象物并设定其相近V，有角透视法，要把对象纳入V1、V2的内侧来画，若要脱离这种规则，需要做若干的调整（图09）。

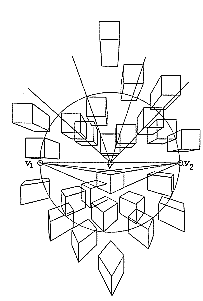
图09

1．视角：
在画透视图时，人的视野可假设为以视点E为顶点圆锥体，它和画面垂直相交，其交线是以C．V．为圆心的圆，圆锥顶角的水平，垂直角为 60°，这是正常视野作的图，不会失真。在平面图上，在视角为60°范围以内的立方体，球体的透视形象真实，在此范围以外的立方体，球体失真变形（图 10、11）。

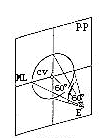
图10

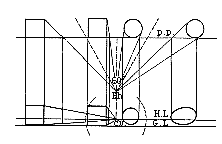
图11

2．视距：
建筑物与画面的位置不变，视高已定，在室内一点透视图中，当视距近时，画面小；当视距远时，画面大。

在立方体的两点透视中，当视距近时，消失点Vx、 Vy距离较小；当视距远时，Vx’、Vy’距离大。即视距越近，立方体的两垂直面缩短越多，透视角度越陡。

建筑物与视点的位置不变，视高已定，若视距近（En和P．P．的距离），则两消失点的间距亦小，透视图形小；若视距远（En和P’．P’．的距离），则两消失点的间距大，透视图形大，两图形相似（图12、13、14）。

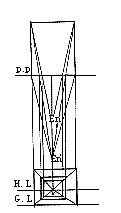
图12

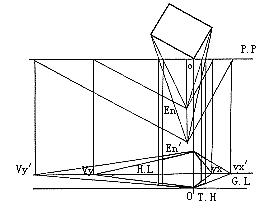
图13

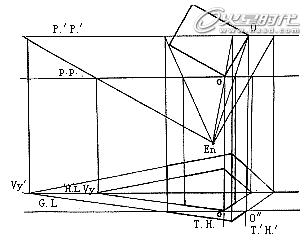
图14

3．视高：
建筑物、画面、视距不变，视点的高低变化使透视图形产生仰视图、平视图和俯视图及鸟瞰图。视高的选择直接影响到透视图的表现形式与效果。如图：上为仰视图，中为平视图，下为俯视图（鸟瞰图）（图15）。

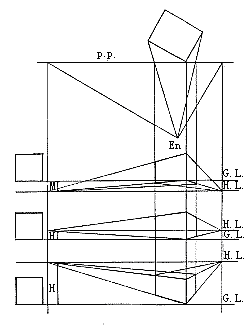
图15

4．透视图形角度：
画面，视点的位置不变，立方体绕着它和画面相交的一垂边旋转，旋转不同角度所成的透视图形。

如图：1和5为立方体的一垂面和画面平行，透视只有一个消失点，在画面上的面的透视为实形。2、3和4为立方体的垂面和画面倾斜，透视图有两个消失点。若垂面和画面交角较小时，则透视角度平缓，交角较大时，则透视角度较陡（图16）。

图16

#p#e#

六、几种透视的基本画法
1．平面投形法：
已知：平面、立面和视点的位置。求：立方体的透视图。
作法：
   1. 根据已知条件，在图纸上画出H．L．、G．L．和其间距H。
   2. 自视点En作OX、OY的平行线，与P．P．相交，交点引垂线，求得Vx、Vy两消失点。
   3. 立方体的一垂边OA在画面上，其透视等于实长。自En向ABCD点连线在画面P．P．上交点，由P．P．上的交点作垂线，引OA=OA’。
   4. 自O、A向Vx、Vy连线求得BB’、DD’。
   5. D点、 B点分别向 Vx、Vy连线求出C点，即可求出立方体透视（图17）。

 
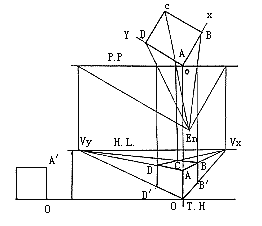
图17

图例1：根据已知立面、平面及视点，求形体透视。先求出Vx、Vy，可得立方体Ⅰ的透视，连接OA求出OA的透视消失点V1，过T．H．量高线间接量出Ⅱ 的透视高度，求出Ⅱ的形体透视（图18）。

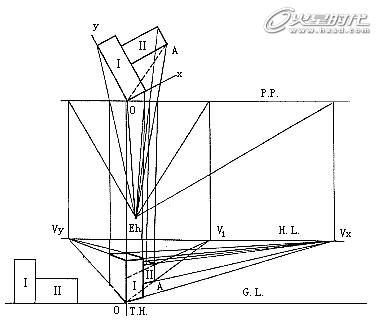
图18

图例2：根据地面上A、B、C任意三点，视高1.2m，人高1.7m，求A、B、C三处人的透视。

作法：任意作一垂线T．H．，和H．L．相交于 D’，量出OD’等于1.2m再加上DD’为0.5m等于人高1.7m。任意在H．L．上取V点，连接D点，O点并延长。由A、B、C各点作水平线与OV 相交，由交点作垂线在DV上的交点引平行线得A’、B’、C’，即得AA’、BB’、CC’三处人高1.7m的透视，这种方法也运用于外观透视图中的人、车等配景（图19、20）。

图19

图20

2．量点法：
一点求法：已知：平面、立面及En点位置，求立方体透视。
作法：
   1. 作OY0=OY，即YY0与P．P．成45°。
   2. 作OY的消失点Vy，YY0的消失点My（量点）。
   3. 在G．L．上量OX0=OX，OY0=OY，连接OVy、X0Vy，连接Y0My与OVy相交Y点，求得平面透视。
   4. 自O点作垂线T．H．，为量高线，量OZ0=ZZ’为立方体真高，求得立方体透视。

实际求法：
1）若视高较低，在G．L．下任意距离作G’．L’．。
2）在H．L．上量VyMy=D，自Vy向右量F，得O点，作透视平面。自各角点引垂线到G．L上，同上述方法求得立方体透视（图21）。

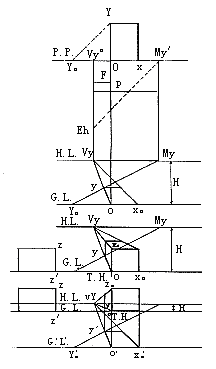
图21

二点求法：已知：平面，立面及En点的位置，求立方体透视。
作法：
   1. 作 OX、OY方向直线透视消失点Vx、Vy。
   2. 以V’x、Vy’为圆心，Vx’En、V’yEn各为半径作圆与P．P．相交求得Mx、My。
   3. 连接  OVx、 OVy，分别为  OX、 OY方向直线的透视方向。
   4. 在G．L．上量OX0=OX，OY0=OY，X0、Y0分别与Mx、My连接，相交于X、Y点。
   5. X、 Y分别与 Vy、 Vx连接求得透视平面。
   6. 在G．L．上由0作T．H．垂线，量OZ0=ZZ’，由Z0分别连接Vx、Vy求得立方体透视。
若视高较低，可在G．L．下任作G’．L．’，先求透视平面。然后由平面上各点引垂线到G．L．上，作出透视图（图22）。

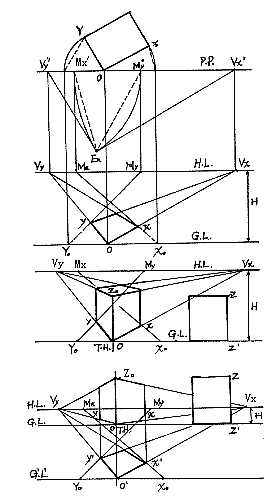
图22

#p#e#

图例一：根据已知平面、立面及En，求形体透视。

作法：
   1. 先求出V’x、 V’y，再分别以V’xEn、V’yEn为半径， V’x、V’y为圆心画圆，求出量点M’y、M’x。
   2. 对应地确定视平线H．L．，地平线G．L，标出Vx、 Vy， Mx、 My，在G．L．下任意距离作 G’． L’。
   3. 以O为圆心分别画圆，求出A、C、D0O点B点落在画面上，再对应地在G’．L’．上确定 A’、B’、C’、D’。
   4. 在画面上各点根据各自有关直线和相交点的消失方向作图，求出平面透视。
   5. 引立面图量高求出形体透视（图23、24）。

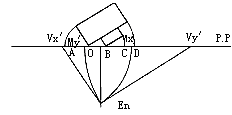
图23

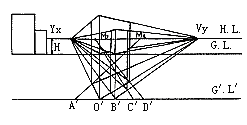
图24

图例二：根据已知平面、立面，求放大n倍的建筑透视图。

作法：
1、在已知平面上作V’x、V’y、M’x、M’y及O点。
2、在透视图H． L上按放大  n倍 nF1、nF2、nF3、nF4的距离，作Vx、Vy、Mx、My，在G．L．上作O点，G．L．以下任作G’L’及O’点。
3、在 G．’L．’上自O’向左量nY2、nY3、nY4、nY1及nX1，向右量nX2、nX3、nX4、nX1及nY1等，自各点分别与My、Mx连线，O’点与Vx、Vy连线求出透视平面。
4、自O点引量高线T．H．放大n倍量出nh1、nh2、nh3。
5、从透视平面中各角点引垂线到相应量高点，连接消失点，即得建筑透视图（图25、26）。

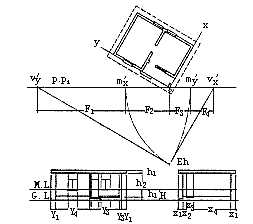
图25

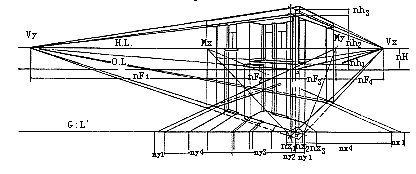
图26

3．灭点法：
根据已知平面、立面，求形体透视。
作法：
   1. 在平面上选定形体与画面的夹角和视点的位置，确定消失点落在P．P．上的位置。
   2. 将平面上的两组直线延伸到P．P．上，以求得它们落在P．P．上的对应点。
   3. 确立视平线、地平线、视高及消失点，自P．P．上各交点作垂线，相应地落到G．L．上。
   4. 在透视图上，根据移到G．L．上的各点，分别向各自的消失点连线，即可得透视平面。
   5. 确定画面上的量高线，找出各角点的垂直高度，即可得形体透视图（图27）。

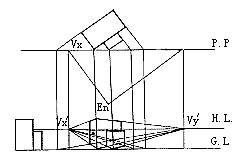
图27

七、斜形透视
通过视点的平面和画面的交线是该平面的透视消失线。凡相互平行的平面，透视消失同一消失线。和画面平行的平面的透视没有消失线。垂直面的透视消失线为一垂线，是过该垂直面上水平线的透视消失点所作的垂线。平行平面上的平行直线的透视消失点在该平行平面的透视消失线上。这种斜形透视形体任何一面都倾向于基面，画法复杂费时，不实用。可用分割和增殖法描绘透视（图28、29、30）。

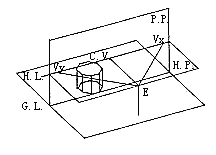
图28

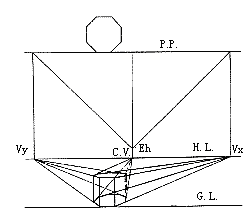
图29

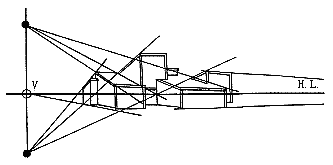
图30

八、分割和增殖
用正方形ABCD上画对角线法可分割成无数的正方形。其中分割的正方形AEFG通过对角线交点的水平线及垂直线的延长上，可增殖无数的正方形。运用这种方法，画透视的立方体，同样可分割或增殖。在建筑物的透视图中，都可起到简便作用。斜形透视图也可用这种方法（图31、32）。

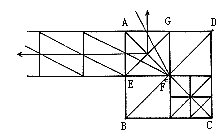
图31

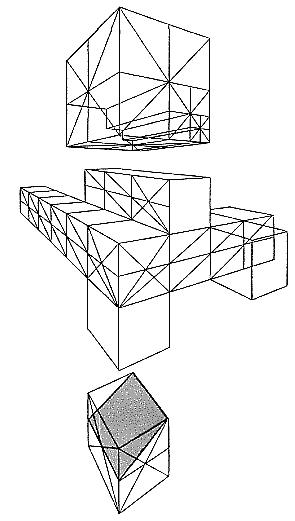
图32