Maya中MEL脚本和表达式的应用解析（四）

◎curve functions (曲线函数)

曲线函数有4个，用于获得一些曲线的信息。

对于这些函数，本书将介绍其中最常用的几个。

01 三角函数。

所谓三角函数，是指一系列描述三角形的边长与夹角关系的函数。三角函数中最常用的是sin(正弦函数) 、cos (余弦函数)、 tg (正切函数) 、ctg( 余切函数)、arc sin (反正弦函数 )和arc cos (反余弦函数)。三角函数之间的关系通常都是用一个直角三角形来描述的，如下图(左)所示。

三角函数几乎是初等数学中最常用，也是变化最多的一组函数，本节只列出了其基本定义的计算公式，更多的变化可以查阅数学方面的书籍，如下图(中)所示。

此处对三角函数的描述并没有区分其中操作对象θ的表示方法，实际上在数学中角度有两种表示方法:度和弧度。对于同一个三角函数，Maya采用不同的函数名来处理不同的角度表示法。

.cos函数

cos函数用来计算一个用弧度表示的角的余弦值。

例如，计算下图(左)所示角θ的余弦值，就是计算边B与C的比值，因此其结果只与角度的大小有关而与三角形的大小无关。在直角三角形中，直角边B不可能大于斜边C,因此cos函数的结果不可能大于1，也不会小于-1。为了更清楚地说明余弦函数的特性，下面来研究:一个特殊的运动。

假设某物体在一个半径为1的圆周路径上进行匀速运动，圆周轨迹的圆心为坐标中心，设两个相互垂直的方向为两个坐标轴方向，物体的运动就变成了绕坐标原点转动。用条线将物体与坐标原点连起来，这条线与x轴形成一个夹角日，如下图(右)所示。对比下图(右)和下图(左)，可以很容易地发现在该物体运动过程中x坐标的变化与夹角θ的关系符合余弦函数的定义。从下图

中可以很直观地看出，物体在整个运动过程中有4个特殊位置:运动轨迹与坐标轴的4个交叉点，这4个特殊位置对应的圆周角为0°、90。、 180 、270，如果 采用弧度表示，就是0弧度、π/2、π、3π/2,对应这4个特殊位置的cos( θ )值分别为1、0、-1、0。

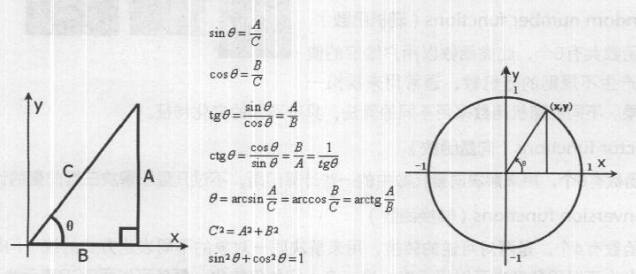
当物体转动超过一周时，运动过程重复。因此，余弦函数是一个周期性函数，其循环周期为2π,如下图所示。

cos函数的一个重要用途就是利用三角形来解决一些问题。先用直角三角形分析运动过程，再利用三角函数进行求解，这是解决数学问题的一种重要方式。

函数格式

float cos(loat number)

在上面的函数格式中，第一个斜体的float说明计算结果为一个浮点数，在实际使用这个函数时不需要书写这一部分;第二部分cos为函数名，这是函数的主体部分;第三部分为一对小括号，对操作对象进行限制，即cos函数只作用于这一对小括号范围内的内容; 第四部分的斜体float与第一部分一样是不需要书写的部分，它表示括号内最后的数据类型;第五部分黑体的number为操作对象，它可以是一个浮点数也可以是一个数学算式，若是一一个数学算式，其计算结果应该是一个浮点数，如果这一部分不是一个浮点数，Maya会自动将它转化成浮点数再进行处理。

实际书写方式如下:

cos(3. 14)、cos(nurbsSphere1.translateX)、 cos(time)、 cos(time*3.0)。

number是用弧度表示的角。COs函数的计算结果类型为浮点数。

函数特殊值

cos(1):结果为0.5403。

cos(π):结果为-1。

cos(0):结果为1.0。

cos(π/2):结果为0。

cos(3π/2):结果为-1.0。

●cosd函数

cosd函数用来计算-一个 用角度表示的角的余弦值。

函数格式

float cosd(float number)

number为用角度表示的角, cosd函数的计算结果类型为浮点数。

cosd函数与cos函数-样，都是余弦函数，所不同的仅仅是操作对象是用弧度表示还是用角度表示。当操作对象采用角度描述时，应该使用cosd函数;用弧度表示时，应该使用cos函数。使用cosd函数时，x坐标轴的单位是度数，如下图所示。

函数特殊值

cosd(0° ):结果为1。

cosd(45° ):结果为0.707。

cosd(90 ): 结果为0。

cosd(180 ):结果为-1。

cosd(270* ):结果为0。

●sin函数。

sin函数用来计算一个 用弧度表示的角的正弦值。下面研究一下物体运动过程中y坐标的变化，如下图(左)所示。

对比上图和下图(中)，可以得到做圆周运动的物体y坐标的变化与图中夹角θ变化存在的相互关系，这种关系用正弦函数来描述。在Maya中，计算正弦值有两个函数sin和sind,如果θ角用弧度来表示，就使用sin函数。sin函数值与θ角的关系如下图(右)所示。

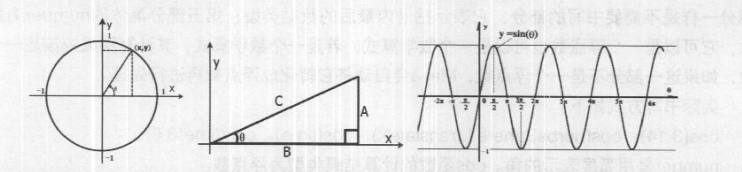
sin函数与cos函数有一些相似之处:函数值在-1~ 1之间;函数值以2π为单位呈周期性变化;当θ为0、π/2、 π、3π/2时， 函数值处于特殊位置上。将两条曲线放在一起进行对比，如5.021所示，可以发现sin函数与cos函数具有完全相同的曲线形状，只是两条曲线在位置上沿θ轴差π/2。

仔细观察下图中正弦函数与余弦函数的曲线，可以看到两条曲线在0~2π之间有两个交点，这两个点也是特殊点，它们对应着45°角(π /4)和225°角(5 π/4)。

函数格式

float sin(float number)

number是用弧度表示的角。sin函数的计算结果类型为浮点数。

函数特殊值

sin(0):结果为0。

sin(π/2):结果为1.0。

sin(1):结果为0.841。

sin(π):结果为0。

sin(3π/2):结果为-1.0。

●sind函数。

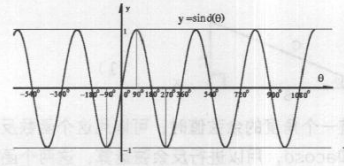
sind函数用来计算一个用角度表示的角的正弦值。sind函数与sin函数样，都是正弦函数，所不同的是操作对象是用角度来表示，如下图所示，这是一张sind函数曲线图。

函数格式

float sind(float number)

number是用角度表示的角，sind函数的计算结果类型为浮点数。

函数特殊值

sind(0°):结果为0。

sind(45° ): 结果为0.707。

sind(90° ): 结果为1.0。

sind(180° ): 结果为0。

sind(270 ): 结果为-1.0。

●tan函数。

三角函数中除了sin (正弦函数)、cos (余弦函数)以外，还有一个重要的三角函数一-tg(正切函数)，如下图所示，其中说明了正切函数与三角形的关系。

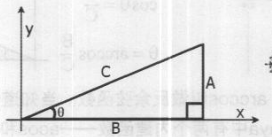
虽然正切函数可以通过正弦函数、余弦函数相除得到，但为了方便使用，Maya还是专为它设了内部函数一tan和tand。 当采用弧度单位描述角的大小时，计算其正切值使用tan函数;当采用角度描述角的大小时，计算其正切值应使用tand函数。在数学教材中，正切函数通常都写作tg,但在Maya中正切函数的函数名为tan或tand。

因为正切函数可以用正弦函数和余弦函数表示出来，正弦函数和余弦函数都是以2π为步长的周期函数，所以tan函数也是一个周期函数，tan函数的循环周期是π。正切函数是正弦函数与余弦函数的商，当θ接近π/2时，作为分母的余弦函数取值趋向0，所以该点的正切函数值从两个方向分别趋向正负无穷，因此正切函数是-一个不连续的函数，如下图所示，这是一张

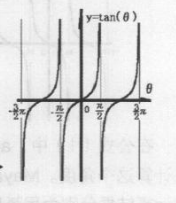函数格式

float tan(float number)

number是用弧度表示的角，tan函数的计算结果类型为浮点数。

函数特殊值

tan(0):结果为0。

tan(π/4):结果为1。

tan(1):结果为1.557。

tan(π/2):结果溢出(此时分母为0，当θ小于并无限接近π/2时，结果趋向正无穷;当θ大于并无限接近π/2时，结果趋向负无穷)。

tan(3π/4):结果为-1。

tan(π):结果为0。

tan(3π/2):结果溢出(显示计算结果错误)。

●tand函数。

tand函数用来计算一个 用角度表示的角的正切值。

与tan函数-样，tand函数也是一一个周期性函数，函数的循环周期是180。。当θ接近90时，作为分母的余弦函数取值趋向0，该点的正切函数值从两个方向分别趋向正负无穷，因此tand函数是-一个不连续的函数。如下图所示，这是tand函数曲线图。

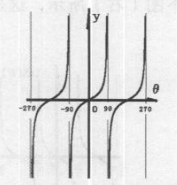
函数格式

float tand(float number)

number是用角度表示的角，tand函数的计算结果类型为浮点数。

函数特殊值

tand(0° ): 结果为0。

tand(45° ): 结果为1。

tand(90 ):结果溢出(此时分母为0 )。

tand(135 ):结果为-1。

tand(180° ):结果为0。

tand(270 ):结果溢出(显示计算结果错误)。

●acos函数。

acos函数与cOs函数是一对计算过程互逆的函数。 在下图所示的直角三角形中，直角边B、斜边C、与B相邻的锐角θ三者之间存在着公式( 1)所表示的对应关系。

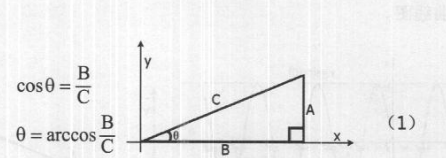
在公式(1)中，arccos叫做反余弦函数。当知道一个角度的余弦值时，可以用这个函数反过来计算这个角度。Maya中有两个内建函数acos和acosd, 用以进行反余弦运算，这两个函数的计算结果分别为用弧度表示的角和用角度表示的角。

如下图所示，这是一张反余弦函数曲线图。图中横坐标是一浮点数，它表示一一个角的余弦值，纵坐标是用弧度表示的角。从图中可以看到，对于一个-1~+1之间的数，有无数个可能的角度。为了确保计算结果的唯一性， 强制规定acos函数值的有效区域为0~ π。

函数格式

float acos(float number)

number是一个-1~ +1之间的浮点数。acos函数的计算结果类型为浮点数，是用弧度表示的一个角的大小，数值在0~ π之间，acos函数的函数曲线如下图所示。

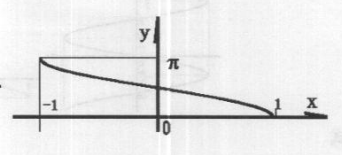
函数特殊值

acos(-1):结果为3.1415( π)。

acos(1.0):结果为0。

acos(0):结果为1.57( π/2)。

acos(0.707):结果为0.7854( π/4)。

●acosd函数。

acosd函数是cosd函数的反函数。

函数格式

float acosd(float number)

number是-一个-1~ +1之间的浮点数。acosd函 数的计算结果类型为浮点数，是用角度表示的一个角的大小，其结果的值域为0。~ 180°。

2.函数特殊值

acosd(-1):结果为180°。

acosd(1.0):结果为0°。

acosd(0):结果为90°。

acosd(0.707):结果为45。

●asin函数。

asin函数是sin函数的反函数，在下图所示的直角三角形中，直角边A、斜边C、与A相对的锐角θ三者之间存在着公式(2)所表示的对应关系。

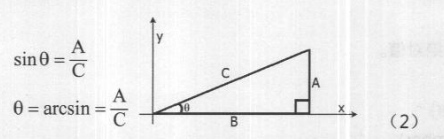
公式(2)中的arcsin叫做反正弦函数。在已知一个角度的正弦函数值时，可以用这个函数反过来计算这个角的大小。Maya中有两个内建函数一-asin和asind, 用以计算反正弦函数，这两个函数的计算结果分别为用弧度表示的角和用角度表示的角。

如下图(左)所示，其中横坐标是一浮点数，它表示一个角的正弦函数值，纵坐标是用弧度表示的角的大小。从下图(左)中可以看到，对于一个-1~+1之间的数，有无数可能的角度与之对应。为了确保计算结果的唯一性，强制规定asin函数值的有效区域为-π/2~ π/2，如下图(右)所示，这是一张asin函数曲线图。

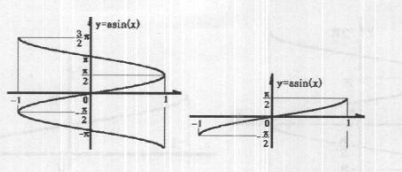
函数格式

float asin(float number)

number是一个-1~+1之间的浮点数。asin函数的计算结果类型为浮点数，是用弧度表示的一个角的大小，其值域在-π/2~ π/2之间。

函数特殊值

asin(-1):结果为-1.57(-π/2)。

asin(0):结果为0。

asin(0.707):结果为0.7854( π/4)。

asin(1.0):结果为1.57 ( π/2)。

asind函数。

asind函数是sind函数的反函数。

函数格式

float asind(loat number)

number是一个-1~ + 1之间的浮点数。asind函 数的计算结果类型为浮点数，是用角度表示的一个角的大小，其值域为-90 ~90°。

函数特殊值

asind(-1):结果为-90。

asind(O):结果为0。

asind(1.0):结果为90°。

asind(0.5):结果为30°。

02 abs函数。

abs函数用来计算绝对值。

●函数格式。

int abs(int number)

float abs(float number)

vector abs(vector number)

abs的计算结果为一个非负数 (正数和0) 。比较特殊的是计算对象 是一个向量型数据时，abs函数对向量的3个分量分别求绝对值，如abs(<<-1.2, 2.2, -0.5>>)的结果为<<1.2, 2.2,0.5>>。

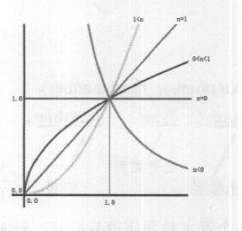
03 pow幕函数。

数学含义

幂函数的数学公式为:

y=x"            公式(3)

这个公式表示对x自乘n次的结果即为y的值，它等价于:

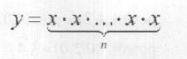
在数学中，与幂函数相似的一一个函数叫做指数函数，其数学公式为:

y=a            公式(4)

指数函数与幂函数的运算方法是相同的，都是某种形式的乘方运算，但二者的不同之处在于幂函数的自变量为乘方运算的底，而指数函数的自变量为乘方运算的指数。

如下图所示，这是幂函数的函数图形。

函数格式

Maya中幂函数和指数函数都是pow()函数。

pow函数的格式为:

pow(base,exponent)

base:底数(浮点数)

exponent:指数(浮点数)

该函数的计算结果也是浮点数。

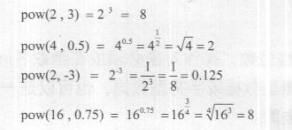
所谓浮点数，是指带小数形式的数字，是与整数相对的形式。虽然在数学计算中4与4.0是一 样的，但在计算机的计算过程中4与4.0是不同的。

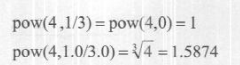
因为指数函数和幂函数具有相似的形式，所以在Maya中并没有对这二者进行区分，都用pow来完成。当指数函数的指数为0.5时，实际上是进行开方运算，Maya中提供了另一个函数一

sqrt,专门进行开方运算。

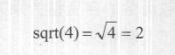
04 min函数。

对两个浮点数进行比较，返回其中较小的一个浮点数。

函数格式

float min(float number float number)

min函数需要两个浮点数，两个浮点数要用逗号分开。计算结果也是一一个浮点数，为输入的两个浮点数中较小的一个。

min(3.4, 4.5): 结果为3.4。

05 max函数。

对两个浮点数进行比较，返回其中较大的一个浮点数。

函数格式

如下图所示。

max函数需要两个浮点数，两个浮点数要用逗号分开。计算结果也是一个浮点数，为输入的两个浮点数中较大的一个。

max(3.4,4.5):结果为4.5。

06 int函数。

在使用数据过程中，应该使数据类型相匹配。当浮点用作整数型时，会截去小数部分。有时候系统自动转化数据类型的结果不能满足需要就要强行改变数据类型。将浮点数取整的种方法就是使用int函数强行改变数据类型。

函数格式

int int(number)

int函数的输出结果是一个整型数， 操作对象必须放在函数名int后面的小括号内。number为操作对象，它可以是浮点数、向量型数据或字符型数据，也可以是一一个计算式。int函数取整的计算方法为截断取整，即将小数部分去除。

int(3.2):结果为3。

int(-2.3):结果为-2。

除了int以外，Maya还提供了ceil函数\floor函数trunc函数.

07 rand函数。

随机函数用来生成一些不规则的数据，这些数据通常用来避免计算结果出现明显的规律。Maya中的随机函数有5个，分别是gauss、noise、 dnoise、 rand和sphrand, 除此之外还有一个随机函数的辅助函数seed,最常用的一个函数就是rand()。

rand函数用来生成一个不确定的数，这个数的大小会在一一个指定范围内。函数自变量就是函数值的取值范围。

rand函数有4种形式，其主要区别在于函数变量不同。rand函数的变量实际上规定了函数值的输出范围,所以rand函数的4种形式实际是函数值域的4种限定方式。

函数格式

形式1: float rand(float maxnumber)

形式1中的maxnumber指明计算结果的最大可能值，其结果最小可能值为0，也就是说这种形式计算结果为一个从0到maxnumber之间的随机数。

形式2: float rand(float minnumber, float maxnumber)

形式2中minnumber和maxnumber直接指定了计算结果的上、下限，minnumber为输出结果的下限，maxnumber为输出结果的上限。

形式3: vector rand(vector maxvector)

形式3中函数变量maxvector为一一个向量，向量的3个分量规定了计算结果向量对应分量的最大值，各个分量的最小值为0，每个分量返回不同的结果。

形式4: vector rand(vector minvector, vector maxvector)

形式4中函数变量maxvector和minvector也是向量，这两个向量的分量分别指定了计算结果向量各分量的最大值和最小值。

形式1和形式2的计算结果都是一个一 元浮点数，形式3和形式4的计算结果都是向量。

实例10:随机函数1

①在命令行中输入rand(5),按下Enter键，在反馈栏中显示出计算结果。

②重复上述操作，结果如下:

rand(5);

// Result: 4.431572 11

rand(5);

// Result: 1.823011 Il

rand(5);

// Result: 0.456653 I1

rand(5);

ll Result: 2.436086 Il

计算结果是一个0~ 5之间的数值。

实例11:随机函数2

按实例5的步骤反复计算rand(1,3),结果如下:

rand(1,3);

// Result: 1.596394 II

rand(1,3);

// Result: 2.751962 I/

rand(1,3);

// Result: 2.063114 I

rand(1,3);

Il Result: 2.840522 II

rand(1,3);

Il Result: 2.030862 I

计算结果是一个1~3之间的数值。

不断重复计算rand(1,- 1)的值，其结果如图所示。

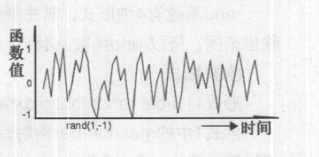
实例12:随机函数3

计算rand(<<1,2,3>>)，反复执行，结果如下:

rand(<<1,2,3>>);

// Result: <<0.542743, 1.335957, 0.513425>> I1

rand(<<1,2,3>>);

// Result: <<0.830779, 1.723811, 2.307663>> //

rand(<<1,2,3>>);

Il Result: <<0.0525795, 1.933459, 1.002852>> I

rand(<<1,2,3>>);

// Result: < <0.0820965, 0.540629, 0.222787>> //

rand(<<1,2,3>>);

// Result: <<0.676226, 1.620317. 1.392634>> /I

计算结果是一个向量，向量的第1个分量是一个0~ 1之间的数，第2个分量是-个0~ 2之间的数，第3个分量是一个0~ 3之间的数。

实例13:随机函数4

计算rand(<<1,2,3>>.<<4,1.5>>),反复执行，结果如下:

rand(<<1,2,3>>.<<4,1.5>>);

// Result: <<3.036632. 1.319077. 4.505413>> //

rand(<<1,2,3>>.<<4.1.5>>);

// Result: << 1.018688, 1.375593, 3.252925>> //

rand(<<1,2,3>>.<<4,1,5>>);

I/ Result: <<2.852649, 1.229072, 3.373072>> //

rand(<<1,2,3>>.<<4.1,5>>);

// Result: <<2 490165, 1.4905, 3.631878>> //

计算结果是一个向量，向量的第1个分量是一个1~ 4之间的数，第2个分量是一个1~ 2之间的数，第3个分量是-个3 ~ 5之间的数。

除了rand函数以外，Maya还提供了另外几个随机函数: gauss函数、 noise函 数、dnoise函数、sphrand函数。

gauss函数虽然也是一-个随机函数，但通过采用完全相同的参数反复计算，然后对计算结果进行统计，就会发现函数值的分布符合gauss (高斯)分布。

noise函数的计算结果有3个明显的特征。

1.函数自变量相同时，计算结果也相同。

2.大小相近的自变量，计算的结果相近。

3.计算结果一定在-1~+1之间。.

dnoise函数的算法与noise-样，但noise的计算结果为一一个单值数据，而dnoise使用一个向量型数据作为函数自变量，计算结果为三元数据，其结果在<<-1.-1,.-1>>到<<1,1,1>>之间。

sphrand函数的计算结果是-个向量，这个向量一定 是在一个由函数变量指定的球体或椭球体中。

08 seed函数。

虽然随机数本身就说明计算结果的不确定性，但也有这种情况:尽管计算结果是随机的、没有规律的，但在某些特殊情况下仍希望重复出现某个随机数，这时就需要用到seed函数。

seed函数可以给gauss , rand和sphrand函数指定-一个计算随机数的种子值，同样的种子值会生成相同的随机数。

int seed(int number)

seed函数的变量值为一个整数。

实例14: seed函数对随机函数的影响

反复计算rand(9)，然后与计算seed函数后再计算rand(9)的结果进行对比。

rand(9);

// Result: 4.273646 //

rand(9);

// Result: 5.030188 //

rand(9);

// Result: 0.42155 //

rand(9);

// Result: 0.571915 // 

rand(9);

// Result: 0.627805 //

seed (9);

rand(9);

// Result: 8. 108162 //

seed (9);

rand(9);

// Result: 8.108162 //

seed (9);

rand(9);

// Result: 8.108162 //

seed (9);

rand(9);

// Result: 8.108162 //

由以上可以看出，在seed函数之后计算随机函数，随机函数的结果就不再是随机的了。

3.表达式与MEL命令

几乎所有初学表达式与脚本的人都会遇到同一个问题一表达式与 脚本的区别。表达式与脚本有许多共同之处，例如都使用程序方式解决问题，都会用到各种语言结构等。有人甚至认为表达式与脚本是一回事，简单一些的叫表达式，复杂一些的就叫脚本。其实这里有一个很大的误解，虽然表达式与脚本有许多共同之处，但二者也有着根本的区别，并不是简单与复杂的关系。

表达式与脚本在以下几个方面有着根本的区别。

01 作用对象。

表达式作用于特定对象，而脚本作用于非特定对象。任何个表达式中-定会写明这个表达式控制的具体物体的具体属性,而脚本却不一定会指定作用于特定物体，常见的一种方式是脚本中指明对当前选择集中的物体进行操作，用户选中不同的物体，脚本就对不同的物体起作用，因此它是面向非固定对象的。

Maya的操作面板实际上都是靠Maya脚本支撑的，所有的操作命令都会调用相应的Maya脚本来完成各自的任务。试想一下， 如果Maya的移动命令只能作用于NURBS小球nurbsSpherel,那会是什么样的结果。

当然，有时候为了完成一些特殊任务， 可能会指定这个脚本只作用于特定的物体，但这种脚本通常并不是一个通用脚本，而是专用脚本。例如在-个项目中，可能到最后的渲染阶段修改了某个角色的材质，要在所有场次、镜头中，将这个角色的材质换成新材质时，就可以写一个专用脚本来实现，这个脚本只能用于这一个角色的材质替换，而不能用于所有角色的材质替换。在做三维项目时，经常需要使用这种专用脚本，而随着这个项目结束，脚本也就失去作用了。

02 作用范围。

表达式与脚本的作用范围是不同的，一个表达式只能作用于一一个场景，而一个脚本却能作用于不同的场景，只要条件符合就能得到正确的结果。

03 作用方式。

场景中的表达式在整个时间范围内控制属性变化，只要场景的当前时间或表达式的输入属性发生了变化，场景中的表达式就会重新计算。表达式的调用并不需要专门的调用命令，只需将表达式编辑保存后，它就会在场景中发挥作用。脚本只有在被调用时，才会对场景起作用，脚本的调用必须使用指定的脚本命令。-般来说，-个脚本在场景中只会被有限次调用，除非是将此脚本写入一个表达式，这样每一帧都会调用此脚本，否则这个脚本不会总是在场景中起作用。

04 保存方式。

虽然在场景内部，表达式是独立的个体，但从保存文件的角度讲，表达式只是场景文件的一部分，并不存在独立的表达式文件，因此表达式是依附于场景文件存在的。脚本是独立于场景文件存在的，所有脚本都保存在独立的脚本文件中，只有在场景中发出了一个脚本命令，相应的脚本才会被调入该场景。在保存场景文件时，该场景会保存脚本作用的结果，而不会保存脚本的作用过程信息，也不会保留该脚本的信息。