学习影视特效需要哪些数学知识？（二）

二、向量

向量（英语：vector，物理、工程等也称作矢量）是数学、物理学和工程科学等多个自然科学中的基本概念，指一个同时具有大小和方向，且满足平行四边形法则的几何对象。一般地，同时满足具有大小和方向两个性质的几何对象即可认为是向量。（特别地，电流属既有大小、又有正负方向的量，但由于其运算不满足平行四边形法则，公认为其不属于向量）向量常常在以符号加箭头标示以区别于其它量。与向量相对的概念称标量或数量，即只有大小、绝大多数情况下没有方向（电流是特例）、不满足平行四边形法则的量。

2.1 表示方法

2.1.1 形式表示

使用符号的形式实际上只是对向量规定的一个概念化代号。向量在包括数学和物理等诸多领域均被广泛采用，优点是简洁明了，缺点是高度形式和抽象，既缺少几何形象性又缺少定量精确性。

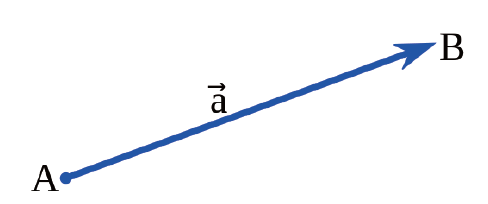
数学上的向量通常可用加向右箭头的小写字母表示，如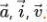 。 有时也有用加箭头的大写字母表示数学量，如微积分中的面积元。 给定两点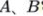时，也可确定一固定向量：如确定一个一个始于点从A 终于点B 的向量，符号表示为：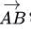

直观上，向量通常被标示为一个带箭头的有向线段。线段的长度表示向量的大小（或称模长），向量的方向即箭头所指的方向，可以记为 。该种表示的优点是具有强烈的几何直观形象性，缺点是在纸面上作图繁琐，不便定量分析。

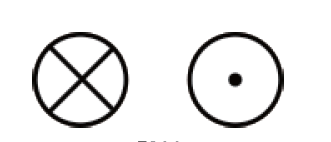
而遇到某些特殊情况（如表示磁场的磁感应强度）需要表示与记载纸面垂直的向量，则会使用圆圈中打叉或打点的方式来表示（如右图）。圆圈中带点的记号（⊙）表示由纸下方指向纸上方的向量，而圆圈中带叉的记号（如左图）则表示由纸的上方指向纸下方的向量。由于这种记号不表示向量的大小，所以必须时需要在旁边或其它地方另外注明。

2.1.3 代数表示

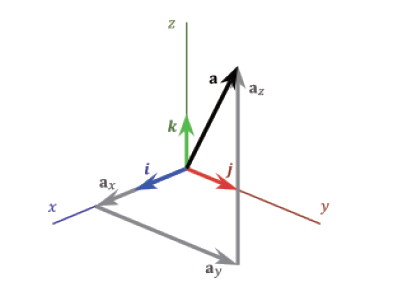
代数表示指在指定了一个坐标系之后，用一个向量在该坐标系下的坐标来表示该向量，兼具了符号的抽象性和几何形象性，因而具有最高的实用性，被广泛采用于需要定量分析的情形。 对于自由向量，将向量的起点平移到坐标原点后，向量就可以用一个坐标系下的一个点来表示，该点的坐标值即向量的终点坐标。

2.2 单位向量

对于任意向量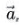不论方向如何，若其大小为单位长度，则称其为方向上的单位向量（Unit vector）。单位向量通常被记为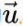

2.3 相反向量

知向量a，如果存在一个向量x，使a+x=0，那么x 叫做a 的相反向量，记作-a，即a+(-a)=0。由向量加法的定义知道，a 与-a 等长而且方向相反， a与-a互为相反向量。

规定，零向量的相反向量仍是零向量。任一向量与其相反向量的和是零向量。

如图有

2.4 零向量

零向量：长度为零的向量叫做零向量，记为0。

三、向量运算

①向量的模的概念

　　所谓的向量的模就是指向量的大小或者说长度。

②向量的模的运算法则

　　在线性代数中，向量的模通常用在向量两边各加两条竖线的方式表

示，如||v||，表示向量v 的模。向量的模的计算公式如下：

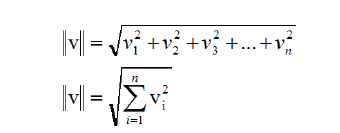
对于2D，3D 向量的如下

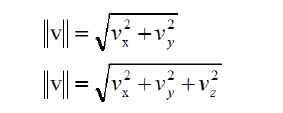
3.1 标量与向量的运算

①运算法则

虽然标量与向量不能相加减，但是可以相乘，至于标量与向量的除法可以看做乘以倒数。

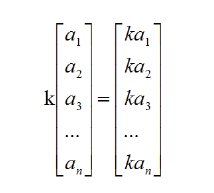
对于2D，3D 向量的如下

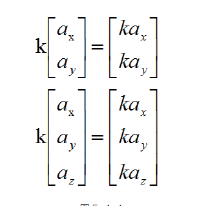
3.2 几何解释

向量乘以标量或者除以标量，相当于以因子k 来缩放向量的长度。

3.3 标准化向量

①. 标准化向量的概念

所谓的标准化向量就是单位向量，就是向量的长度为1 的向量。有时候也称作为法线。

②. 运算法则

对于任意非零向量v，都能计算出一个和v 方向相同的单位向量n，这个过程被称作为向量的“标准化”，要标准化向量，将向量除以它的大小（模）即可。

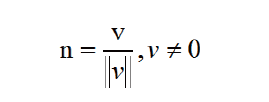
3.4 向量的加法和减法

① 向量的加法和减法的前提

如果两个向量的维数相同，那么他们能够相加减，运算结果的向量的维数和原向量相同。向量的加法等于两个向量的分量相加，向量的减法相当于加上一个负向量。

3.5 运算法则

向量的加法等于两个向量的分量相加，向量的减法相当于加上一个负向量。

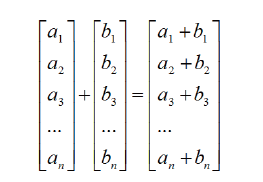
3.6 几何解释

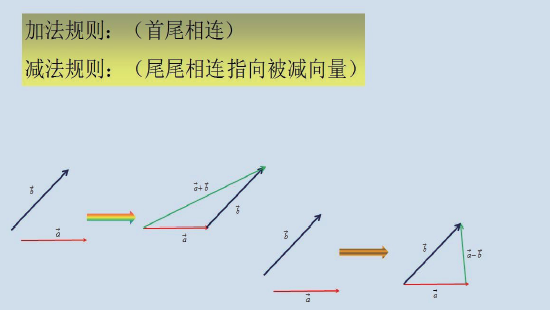
向量的加法和减法引导出了三角形法则，即将向量的首尾相连就会得到加法的结果，如下。

3.7 距离公式的推导

通过上面的三角形原则，我们可以发现，通过两个向量的加减可以得到第三个向量，我们将这个过程逆置，如果知道了两点的距离，如何求出其距离，我们可以利用向量的减法实现。

运算公式：

在3D 中，已知两点a，b，求两点之间的距离d ？我们可以将a，b 两点看做向量，然后b-a 就是向量d，然后我们再计算向量d 的模就是两点间的距离。

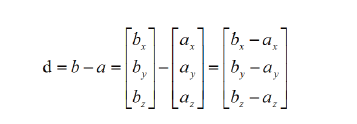
求出向量d 后，再求d 的模就是两点的距离。

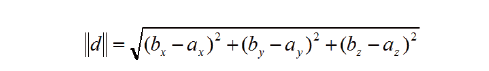
3.8 向量的点乘

3.8.1 基本概念

标量可以和向量相乘，向量也可以和向量相乘，这就叫点乘，也叫做内积。标量与向量相乘不可以写点， 向量与向量相乘必须要写点，向量的点乘优先级高于向量的加减法。注意：向量点乘后的结果是标量。

3.8.2 运算法则

注意：向量点乘后的结果是标量，不再是向量。

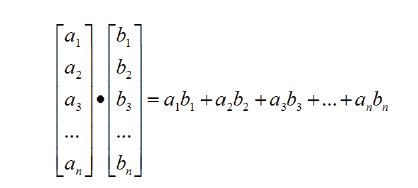
应用到2D，3D 中为

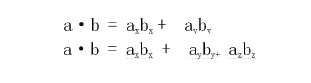
3.8.3 几何解释

向量的点乘描述的是两个向量的相似程度，即两个向量之间的夹角的大小向量的点乘的集合运算法如下， 向量的点乘结果与cos 函数有关，当两个向量垂直时，向量的点乘结果为0。

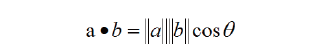
3.9 向量的投影

3.9.1 基本概念

给定两个向量v 和n，能将v 分解成两个分量，一个是垂直于向量n，一个平行于向量n，平行于向量n的向量我们称为在向量n 上的投影。

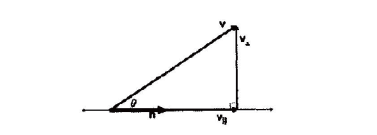
3.9.2 投影的求解

因为向量n 平行于投影向量，所以可以求出向量n 的单位向量再乘以投影的模，就可以得到投影向量， 如下：

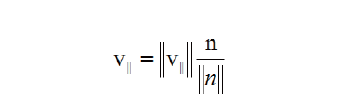
我们接下来求投影的模即可，我们可以根据三角函数的余弦公式来求出投影的模

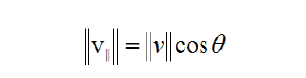
代入投影的模就可以求出投影向量

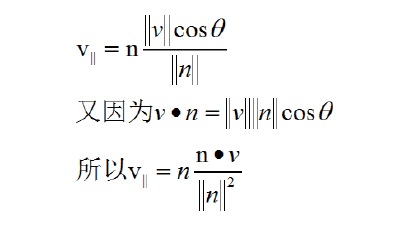
3.10 垂直向量的求解

根据三角形法则，可以轻易求出垂直的向量

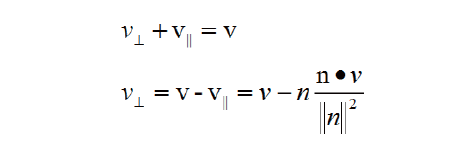
3.11 向量的叉乘

3.11.1 基本概念

两个向量的叉乘得到是向量，且这个向量垂直于原来的两个向量。向量的叉乘只可以运用在3D 向量中。

3.11.2 数学运算公式

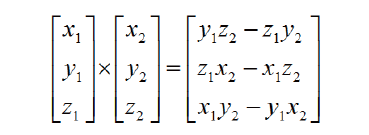
3.11.3 几何运算公式

向量叉乘的结果向量的长度与两个向量的夹角有关，且成正弦函数关系，如果向量a 和b 是平行关系，则叉乘的结果为0，因为sin0 为0

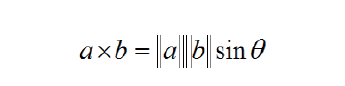
3.11.4 向量叉乘方向的判断

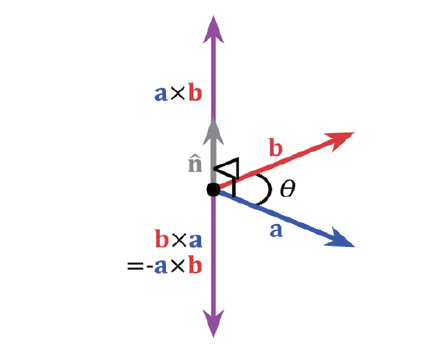
向量的叉乘是通过右手定则来判断结果向量的方向的。伸出右手，四指弯曲符合向量叉乘的顺序，那么大拇指就是叉乘后结果向量的方向。如下图axb，右手四指弯曲方向从a 到b，大拇指方向向上就是叉乘结果向量的方向。